Here we will learn about sine graphs, including how to recognise the graph of the sine function, sketch the sine curve and label important values, and interpret the sine graph.
There are also sine graphs worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
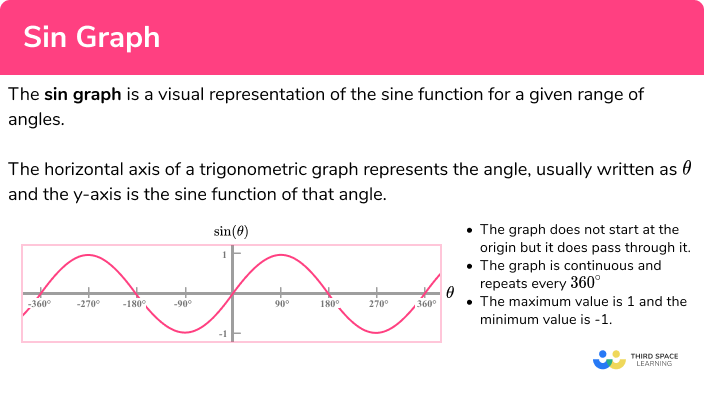
The sin graph is a visual representation of the sine function for a given range of angles.
The horizontal axis of a trigonometric graph represents the angle, usually written as \theta , and the y -axis is the sine function of that angle.
We will only look at the graph of the sine function in this lesson for angles in degrees although this can also be represented in radians.

Remember that \sin(\theta) is a relationship between the opposite side and the hypotenuse of a right angle triangle:
Let’s look at 3 triangles where we would use the sine ratio to calculate the size of the angle \theta . For each triangle, the hypotenuse is the same but the length of the opposite side and the associated angle change.
Here we can see that as \sin(\theta)=\frac , as the angle \theta increases, the length of the side opposite to the angle also increases. So for each triangle we have:
So what would happen if the opposite side to the angle is equal to 10 ?
So when the opposite side is equal to the hypotenuse, we get \sin(\theta) = 1 .
What about when the opposite side is equal to 0 ?
So when the opposite side is equal to 0, \; \sin(\theta) = 0.
If we plotted a graph to show the value of \sin(\theta) for each value of \theta between 0^o and 90^o , we get the following graph of the sine function:
Let us add the values of \sin(\theta) for the three triangles from earlier into the graph to show how they would look:
We can now use the graph to find the angle \theta for triangles 1, 2, and 3 :
This graph shows that when \sin(\theta) = 0.2 , \; \theta = 12^o so we have the triangle
This graph shows that when \sin(\theta) = 0.6 , \; \theta = 37^o so we have the triangle
This graph shows that when \sin(\theta) = 0.9 , \; \theta = 64^o so we have the triangle
This shows us that we can use the graph of the sine function to find missing angles in a triangle. More on this later as we have a large problem to resolve. How can the opposite side of a right angle triangle be the same as the hypotenuse, or equal to 0 ?
Unfortunately there is a limit to the use of trigonometric ratios to find angles between 0 and 90^o . For any larger or smaller angles, we need to look at the unit circle.

The unit circle is a circle of radius 1 with the centre at the origin. We can label the values where the circle intersects the axes because we know that the radius of the unit circle is 1 unit.
We can still construct a triangle within the unit circle with the angle starting from the positive x axis.
Looking at the trigonometric ratios of sine and cosine, we can say that:
This means that the width of the triangle is equal to \cos(\theta) and the height of the triangle is equal to \sin(\theta) . The point on the unit circle is therefore the coordinate ( \cos(\theta) , \; \sin(\theta) ):
The y value of the coordinate on the unit circle gives us the value for \tan(\theta) so:
\sin(\theta) is as periodic function as we could continue to turn around the origin from the positive x axis beyond 360^o . We can also turn anticlockwise which would give us the negative value for the value of \sin(\theta) . The period of the function is 360^o .
From the unit circle, we can see that the angle \theta gives a positive value for y when the angle \theta is between 0^o and 180^o .
Between 180^o and 360^o , the y value is negative, and so \sin(\theta) is negative.
Visualising this using a coordinate axes, we can show when \sin(\theta) is positive and negative:
We are no longer limited to the range of values for \theta as we can continue to turn any angle, in a positive or negative direction and obtain a value for \sin(\theta) . We can therefore expand the graph drawn previously to represent this new set of values on a graph for angles between -360^o and 360^o .
You should be able to interpret the unit circle to determine the value of \theta .
Here are a couple of examples to help you.
Top tip: you can remember the coordinate order as alphabetical; x before y and cos before sin to get the coordinate (\cos(\theta), \; \sin(\theta))
Now that we have generated the graph of \sin(\theta) , we need to be able to interpret it to find values of \theta and \sin(\theta) for any value between the range -360^o \leq \theta \leq 360^o (values for \theta between -360^o and 360^o .
The inverse function to \sin(\theta) is \sin^(\theta) .
The notation used for inverse functions should not be confused with the reciprocal function. In A level Mathematics, we learn that the reciprocal function to \sin(\theta) is called the cosecant or \cosec(\theta) where \cosec(\theta)=\frac .
The graphs of \sin \theta and \cos \theta are very similar. In fact, if you applied a phase shift to either graph, you will get the graph of the other function.
Graphing the functions of y=\sin(\theta) (in green) and y=\cos(\theta) (in blue):
If we moved the graph of \cos \theta to the right by subtracting 90 degrees from every angle (\cos(\theta+90)) we get \sin(\theta) . This horizontal shift can be in either direction. We can also carry out a vertical shift, a horizontal stretch, a vertical stretch, a rotation, and more!
In order to use sine graphs:

Get your free sine graph worksheet of 20+ sine, cosine & tangent graphs questions and answers. Includes reasoning and applied questions.


Get your free sine graph worksheet of 20+ sine, cosine & tangent graphs questions and answers. Includes reasoning and applied questions.
Use the graph of \sin(\theta) to estimate the value for \theta when \sin(\theta)=1 for 0^o \leq \theta \leq 90^o
2 Draw a straight, perpendicular line at the intersection point to the other axis.
3 Read the value where the perpendicular line meets the other axis.
When \sin(\theta)=1, \; \theta=90^o
Use the graph of \sin(\theta) to estimate the value for \theta when \sin(\theta)=-0.4 for 90^o \leq \theta \leq 270^o
Draw a straight line from the axis of the known value to the sine curve.
Draw a straight, perpendicular line at the intersection point to the other axis.
Read the value where the perpendicular line meets the other axis.
When \sin(\theta)=-0.4, \; \theta=204^o
Use the graph of sin(\theta) to estimate the value for \sin(\theta) when \theta=186^o .
Draw a straight line from the axis of the known value to the sine curve.
Draw a straight, perpendicular line at the intersection point to the other axis.
Read the value where the perpendicular line meets the other axis.
When \theta=186^o, \; \sin(\theta)=-0.1 .
Use the graph of \sin(\theta) to estimate the value for \theta when \sin(\theta)=0 for -180 \leq \theta \leq 0^o
Draw a straight line from the axis of the known value to the sine curve.
Draw a straight, perpendicular line at the intersection point to the other axis.
Read the value where the perpendicular line meets the other axis.
When \sin(\theta)=0, \; \theta=-180^o and \theta =0^o
Use the graph of \sin(\theta) to estimate the value for \sin(\theta) when \theta=-307^o .
Draw a straight line from the axis of the known value to the sine curve.
Draw a straight, perpendicular line at the intersection point to the other axis.
Read the value where the perpendicular line meets the other axis.
When \theta=-307^o, \; \sin(\theta)=0.8 .
Use the graph of \sin(\theta) to estimate the value for \theta when \sin(\theta)=-0.6 for -360^o \leq \theta \leq 360^o
Draw a straight line from the axis of the known value to the sine curve.
Draw a straight, perpendicular line at the intersection point to the other axis.
Read the value where the perpendicular line meets the other axis.
When \sin(\theta)=-0.6, \; \theta= 143^o, \; \theta=-37^o, \; \theta=217^o \; \text \; \theta=323^o
When you are finding the value of \theta using a trigonometric graph, only one value is calculated when there are more points of intersection.
E.g. Only the value of 65^o is read off the graph.
The sine and cosine graphs are very similar and can easily be confused with one another. A tip to remember is that you “sine up” from 0 for the sine graph so the line is increasing whereas you “cosine down” from 1 so the line is decreasing for the cosine graph.
The tangent function has an asymptote at 90^o because this value is undefined. As the curve repeats every 180^o , the next asymptote is at 270^o and so on.
Each trigonometric graph is a curve and therefore the only time you are required to use a ruler is to draw a set of axes. Practice sketching each curve freehand and label important values on each axis.
When finding a value of \theta using a trigonometric graph, you must make sure that the value of \theta is within the range specified in the question.
For example, the range of values for \theta is given as 0^o \leq \theta \leq 270^o . Only the value of \theta=240^o is valid for the solution, whereas the solution \theta=300^o would be correct for the range 0^o \leq \theta \leq 360^o , it is not valid for this situation.
Sin graph is part of our series of lessons to support revision on trigonometry. You may find it helpful to start with the main trigonometry lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
1. Use the graph of \sin(\theta) to calculate the value of \theta when \sin(\theta)=0.26 for 0^o \leq \theta \leq 180^o